外观
Chapter 2 数理统计
约 7343 字大约 24 分钟
2025-09-17
Part 1 大数定理与中心极限定理
· 切比雪夫不等式
设随机变量 X 的期望为 E(X),方差为 D(X),则对于任意给定的 ϵ>0,有:
P{∣X−E(X)∣≥ϵ}≤ϵ2D(X)
或等价地
P{∣X−E(X)∣<ϵ}≥1−ϵ2D(X)
说明:
- 该不等式给出了随机变量偏离期望值的概率上界
- 方差 D(X) 越小,偏离概率的上界越小
- 适用于任何具有有限方差的随机变量
· 大数定律
大数定理:在大量重复试验中,样本平均数会趋近于理论期望值。换句话说,当试验次数足够多时,实验结果的平均值会接近预期的长期平均值。
切比雪夫大数定律 (Chebyshev's LLN).
条件:
- 随机变量序列 X1,X2,⋯,Xn,⋯ 相互独立
- 数学期望 EXi 和方差 DXi 都存在
- 方差有公共上界:DXi≤c (i=1,2,⋯)
结论: 对任意 ϵ>0,有
n→∞limP{n1i=1∑nXi−n1i=1∑nEXi<ϵ}=1
核心思想: "只要方差有限,大量重复试验的平均值会接近期望值"
伯努利大数定律 (Bernoulli's LLN).
条件: 设 Xn∼B(n,p),μn 是 n 次伯努利试验中事件 A 发生的次数
结论: 对任意 ϵ>0,有
n→∞limP{nμn−p<ϵ}=1
核心思想: "投硬币这类事情,大量地实验结果里,频率会接近概率"
辛钦大数定律 (Khinchin's LLN).
条件: 随机变量序列 X1,X2,⋯,Xn,⋯ 相互独立同分布,且 EXi=μ
结论: 对任意 ϵ>0,有
n→∞limP{n1i=1∑nXi−μ<ϵ}=1
核心思想: "同一类型的随机变量,大量样本的平均值会接近期望值"
· 中心极限定理
n个随机变量X1,X2,X3,⋯,Xn,它们相互独立且服从同一种分布规律(独立同分布),期望值为μ,方差为D,有:
nD∑i=1nXi−nμ∼N(0,1)ori=1∑nXi∼N(nμ,nD)
D/nX−μ∼N(0,1)orX∼N(μ,nD)
Part 2 数理统计基本概念
· 总体与样本
总体:研究对象某项数量指标的全体称为总体。构成总体的每个成员称为个体。例如,研究一批机器的寿命,则全部机器的寿命构成问题的总体,每一台机器的寿命是一个个体,总体是寿命 X 服从的分布。
注:总体分布的类型有时是明确的,统计的任务是确定未知参数,即参数估计;有时是不明确的,需要先对分布进行假定,再估计未知参数。
样本:在相同条件下对总体 X 进行 n 次简单随机抽样,得到的 n 个观察结果 X1,X2,…,Xn 相互独立且同分布于总体 X ,称 X1,X2,…,Xn 为来自总体 X 的一个简单随机样本,简称样本,其中 n 称为样本容量。抽样得到的一组实数记为 x1,x2,…,xn ,称为样本观察值,简称样本值。
例如,从该批机器中随机抽 20 台测定其寿命,即得容量为 20 的样本观测值 x1,x2,…,x20 。抽取前无法预知每台样品的寿命,因此样本 X1,X2,…,X20 是随机变量。
- 有些教材中为简单化处理,统一用 x1,x2,…,xn 表示样本和样本值。
- 从总体中抽样的方法是多种多样的,本课程仅研究简单随机样本,即 X1,X2,…,Xn 相互独立且同服从于总体分布。
· 经验分布函数
定义 设 X1,X2,…,Xn 为总体 X 的一个样本,其样本值为 x1,x2,…,xn ,则称函数
Fn(x)=n{Count of x1,x2,…,xn less than or equal to x}(−∞<x<+∞)
为样本值 x1,x2,…,xn 的经验分布函数。
若已知样本值 x1,x2,…,xn 的频数、频率分布表为
指标 X x1∗ x2∗ ... xl∗ 频数 ni n1 n2 ... nl 频率 fi nn1 nn2 ... nnl 则经验分布函数
Fn(x)=⎩⎨⎧0,nn1+⋯+ni,1,x<x1∗,xi∗≤x<xi+1∗,(i=1,2,…,l−1)x≥xl∗.
格里文科定理:对于任意实数 x ,当 n→∞ 时 Fn(x) 以概率 1 一致收敛于分布函数 F(x) 。即当 n 充分大时,经验分布函数的任一个观察值 Fn(x) 是总体分布函数 F(x) 的良好近似,从而实际上可当作 F(x) 来使用。
· 统计量
定义:不含任何未知参数的样本函数 g(X1,X2,…,Xn) 称为统计量。设 x1,x2,…,xn 是对应于样本 X1,X2,…,Xn 的样本值,则称 g(x1,x2,…,xn) 是 g(X1,X2,…,Xn) 的观测值,称为统计值。
常用统计量:
设 X1,X2,⋯,Xn 为总体 X 的一个样本, n 为样本容量
- 样本均值
X=n1i=1∑nXi
- 样本方差
S2=n−11i=1∑n(Xi−X)2=n−11(i=1∑nXi2−nX2)
推导过程
S2=n−11i=1∑n(Xi−X)2=n−11i=1∑n(Xi2−2XiX+X2)=n−11(i=1∑nXi2−2Xi=1∑nXi+nX2)
=n−11(i=1∑nXi2−2nX2+nX2)=n−11(i=1∑nXi2−nX2)
- 样本标准差
S=S2=n−11i=1∑n(Xi−X)2
- 样本 k 阶原点矩
Ak=n1i=1∑nXik,k=1,2,…,
- 样本 k 阶中心矩
Bk=n1i=1∑n(Xi−X)k,k=1,2,…,
· 样本统计量的数字特征
已知 X1,X2,⋯,Xn 为来自总体 X 的样本, EX=μ,DX=σ2
EXi=μ,DXi=σ2
EX=μ,DX=nσ2
ES2=DX
· 三大抽样分布
χ2 **卡方分布 (Chi-square Distribution) **
定义 设 X1,X2,⋯,Xn 是来自总体 N(0,1) 的样本,则称统计量
χ2=X12+X22+⋯+Xn2
服从自由度为 n 的 χ2 分布,记为 χ2∼χ2(n) 。
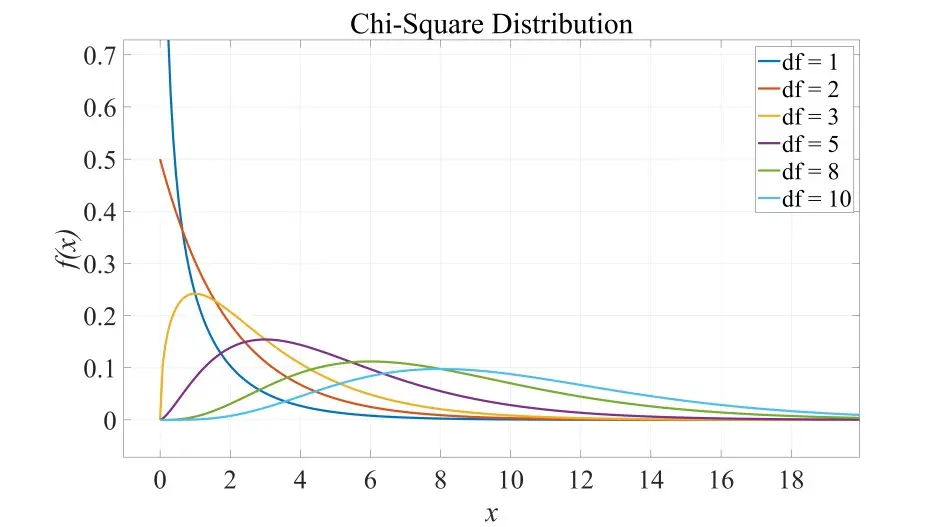
性质
- 可加性:设 χ12∼χ2(n1) , χ22∼χ2(n2) ,并且 χ12 , χ22 独立,则
χ12+χ22∼χ2(n1+n2)
数学期望和方差(背):若 χ2∼χ2(n) ,则有 EX=n , DX=2n
分位点
分位点定义 设有分布函数 F(x) ,对给定的 α(0<α<1) ,若有
P{X>xα}=α
则称点 xα 为 F(x) 的上 α 分位点。
χ2(n) 的分位点 设 χ2∼χ2(n) ,对给定的 α(0<α<1) ,若有 χα2(n)>0 满足
P{χ2>χα2(n)}=α
则称 χα2(n) 为 χ2(n) 分布的上 α 分位点。
t分布 (Student's t-Distribution)
定义 设 X∼N(0,1) , Y∼χ2(n) ,且 X,Y 独立,则称随机变量
t=Y/nX
服从自由度为 n 的 t 分布,记为 t∼t(n)
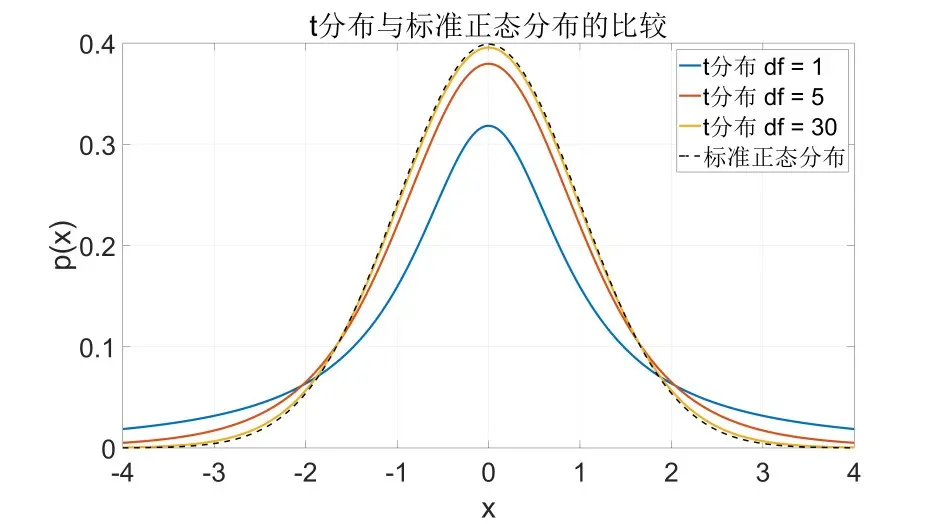
性质
奇偶性: t 分布的概率密度 f(t) 图像为偶函数。
分位点 对于给定的 α(0<α<1) ,称满足条件 P{t>tα(n)}=α 的点 tα(n) 为 t(n) 分布的上 α 分位点。易得
t1−α(n)=−tα(n)
结论
- 自由度 n=1 的 t 分布是标准柯西分布,它的期望不存在。
- 自由度 n>1 的 t 分布期望存在且为 0。
- 当自由度较大( n≥30 )时, t 分布与标准正态分布 N(0,1) 近似。
F分布 (F-Distribution)
定义 设 X∼χ2(n1) , Y∼χ2(n2) ,且 X,Y 独立,则称随机变量
F=Y/n2X/n1
服从自由度为 (n1,n2) 的 F 分布,记为 F∼F(n1,n2) , n1 称为第一自由度, n2 称为第二自由度。
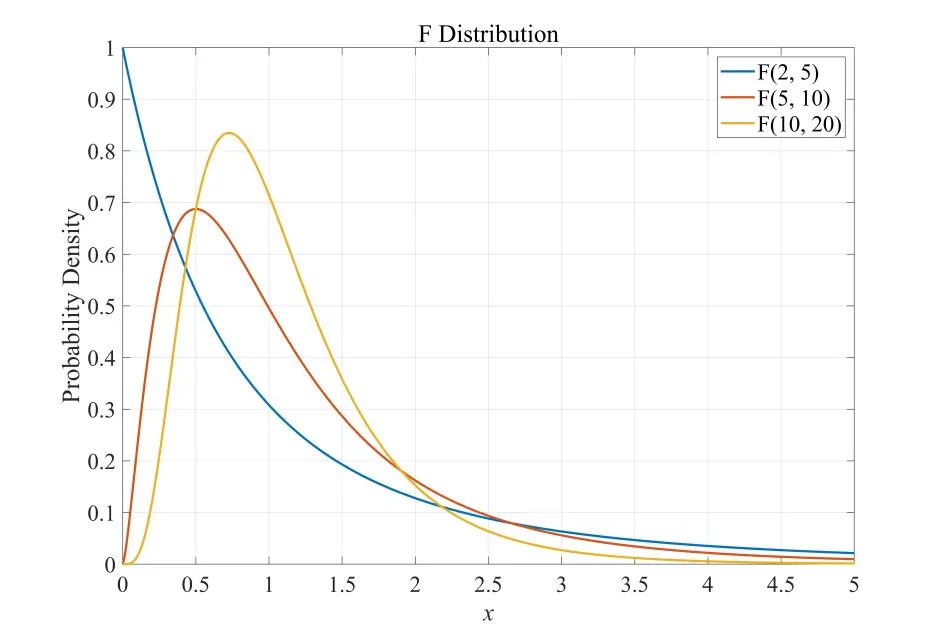
性质:若 F∼F(n1,n2) ,则
F1∼F(n2,n1)
分位点:对于给定的 α(0<α<1) ,称满足条件 P{F>Fα(n1,n2)}=α 的点 Fα(n1,n2) 为 F(n1,n2) 分布的上 α 分位点。易得
F1−α(n1,n2)=Fα(n2,n1)1
· 分位点
/Definition/
分位数定义:对于遵循某个分布的随机变量 X,给定一个参数 α(0<α<1),如果存在一个值X0满足:
P{X>X0}=α
则称 X0 为该分布的上 α 分位点。
不同分布的上 α 分位点表示
卡方分布:上 α 分位点记为 χα2(n).
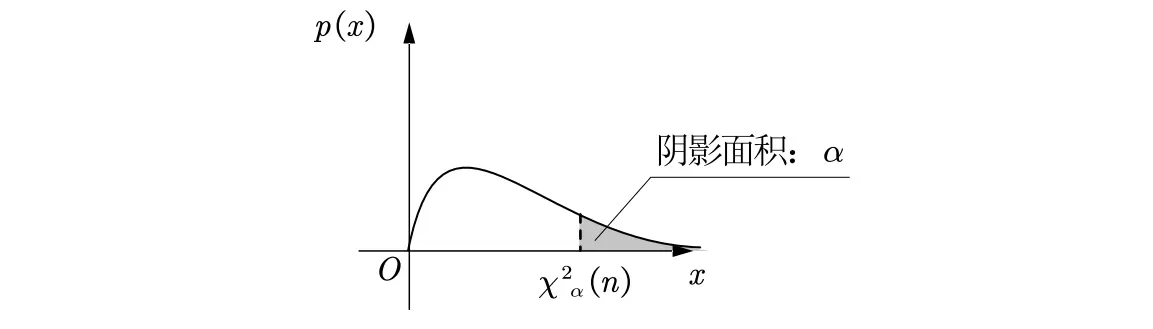
t分布:上 α 分位点记为 tα(n).
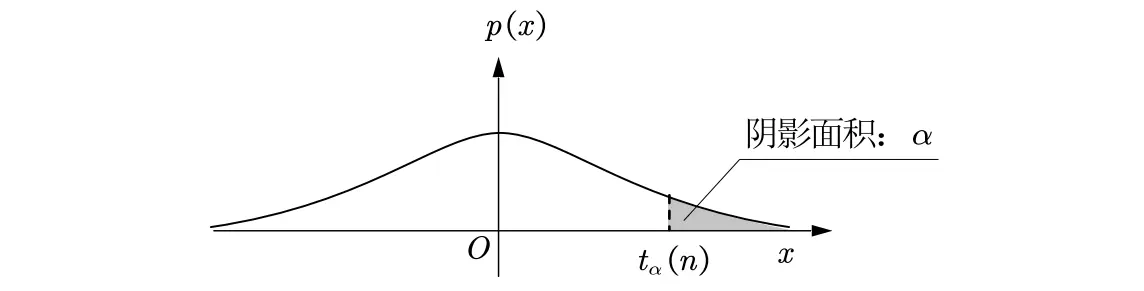
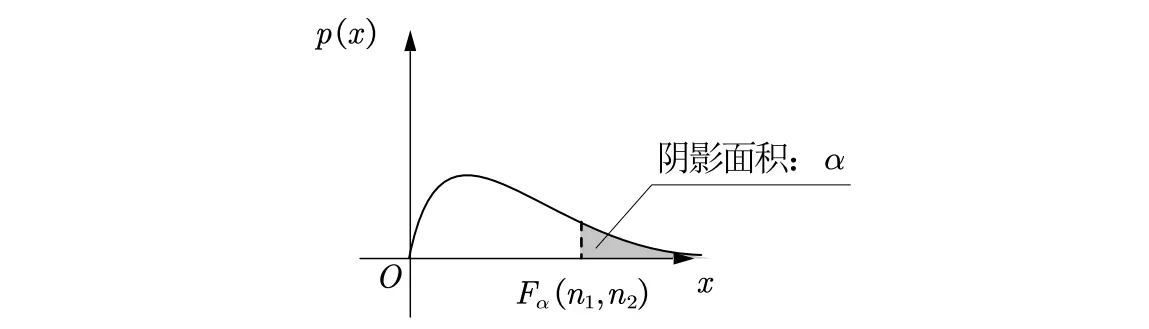
F分布:上 α 分位点记为 Fα(n1,n2).
· 正态总体抽样分布
一个正态总体:假设 X1,X2,⋯,Xn 是来自正态总体 X∼N(μ,σ2) 的样本,样本均值与样本方差分别是
X=n1i=1∑nXiS2=n−11i=1∑n(Xi−X)2
X∼N(μ,nσ2)⇒σ/nX−μ∼N(0,1)
样本均值 X 与样本方差 S2 相互独立;
σ2(n−1)S2=σ2∑i=1n(Xi−X)2∼χ2(n−1);σ2∑i=1n(Xi−μ)2∼χ2(n);
T=S/nX−μ∼t(n−1)
两个正态总体:
设 X1,⋯,Xn1 是取自总体 X∼(μ1,σ12) 的一个样本, Y1,⋯,Yn2 是取自总体 Y∼(μ2,σ22) 的一个样本,且这两个样本相互独立,即假定 X1,⋯,Xn1,Y1,⋯,Yn2 是 n1+n2 个相互独立的随机变量,则有
n1σ12+n2σ22(X−Y)−(μ1−μ2)∼N(0,1)
证明:
X∼N(μ1,n1σ12),Y∼N(μ2,n2σ22)
X 与 Y 相互独立,故
X−Y∼N(μ1−μ2,n1σ12+n2σ22)
标准化有
n1σ12+n2σ22(X−Y)−(μ1−μ2)∼N(0,1)
S22/σ22S12/σ12∼F(n1−1,n2−1)
证明:
σ12(n1−1)S12∼χ2(n1−1),σ22(n2−1)S22∼χ2(n2−1)
,且它们相互独立,故
σ12(n1−1)S12/(n1−1)/(n2−1)S22/(n2−1)S22/σ22=S22/σ22S12/σ12∼F(n1−1,n2−1)
当 σ12=σ22=σ2 时,有
Sw⋅n11+n21(X−Y)−(μ1−μ2)∼t(n1+n2−2)
其中
S12=n1−11i=1∑n1(Xi−X)2,S22=n2−11i=1∑n2(Yi−Y)2,Sw2=n1+n2−2(n1−1)S12+(n2−1)S22
证明:由
σ2(n1−1)S12∼χ2(n1−1),σ2(n2−1)S22∼χ2(n2−1)
,且相互独立,根据可加性,
σ2(n1−1)S12+σ2(n2−1)S22=σ2(n1+n2−2)Sw2∼χ2(n1+n2−2)
由
σn11+n21(X−Y)−(μ1−μ2)∼N(0,1)
,且 X−Y 与 Sw2 相互独立,故
σn11+n21(X−Y)−(μ1−μ2)⋅Sw⋅n11+n21σ=Sw⋅n11+n21(X−Y)−(μ1−μ2)∼t(n1+n2−2)
Part 3 参数估计
· 点估计
点估计
设 θ 是总体 X 的未知参数,用统计量 θ^=θ^(X1,X2,⋯,Xn) 来估计 θ ,称为 θ 的估计量。对于样本的一组观察值 x1,x2,⋯,xn ,代入 θ^ 的表达式中所得的具体数值称为 θ 的估计值。这样的方法称为参数的点估计。
矩估计
用样本矩去估计相应总体矩,或者用样本矩的函数去估计总体矩的同一函数的估计方法就是矩估计。
设总体 X 的概率分布中含有 m 个未知参数 θ1,θ2,⋯,θm 。假定总体的 k 阶原点矩存在,记
μk=E(Xk)(k=1,2,⋯,m),Ak=n1i=1∑nXik
为样本 k 阶矩,令
μk(θ1,θ2,⋯,θm)=Ak (k=1,2,⋯,m)
则此方程组的解 (θ^1,θ^2,⋯,θ^m) 称为参数 (θ1,θ2,⋯,θm) 的矩估计量。矩估计量的观察值称为矩估计值。
最大似然估计(极大似然估计)
(1) 设总体 X 的概率分布为 p(x;θ) (当 X 为连续型时,其为概率密度函数,当 X 为离散型时,其为分布律), θ=(θ1,θ2,⋯,θm) 为未知参数, x1,x2,⋯,xn 为样本观察值,则
L(x1,x2,⋯,xn,θ)=i=1∏np(xi;θ)=L(θ)
称为 θ 的似然函数。
(2) 对给定的 x1,x2,⋯,xn ,使似然函数达到最大值的 θ^(x1,x2,⋯,xn) 称为 θ 的最大似然估计值,相应地 θ^(X1,X2,⋯,Xn) 称为 θ 的最大似然估计量。
(3) 最大似然估计的常用求解方法:由于 lnL(θ) 与 L(θ) 有相同的最大值点,若 L(θ) 可导,则可由对数似然方程组
∂θi∂lnL(θ1,θ2,⋯,θm)=0(i=1,2,⋯,m)
求出 θi 的最大似然估计量。需注意的是这一方法并不都是有效的,对于有些似然函数,其驻点或导数不存在,这时应考虑用其他方法求似然函数的最大值点。
· 估计量的评选标准
无偏性 设 X1,X2,⋯,Xn 为来自总体 X 的样本, θ^ 为 θ 的一个估计量,如果 E(θ^)=θ 成立,则称估计量 θ^ 为参数 θ 的无偏估计。
有效性 设 θ^1,θ^2 都为参数 θ 的无偏估计量,若 D(θ^1)≤D(θ^2) ,则称 θ^1 比 θ^2 有效。特别地,若对于 θ 的任一无偏估计量,都有 D(θ^1)≤D(θ^) ,则称 θ^1 是 θ 的最小方差无偏估计(最佳无偏估计)。
一致性 设 θ^ 为未知参数 θ 的估计量,若对任意给定的 ε>0 ,都有
n→∞limP(∣θ^−θ∣<ε)=1
即 θ^ 依概率收敛于参数 θ ,则称 θ^ 为 θ 的一致估计或相合估计。
· 区间估计
区间估计
设 θ 为总体的未知参数, θ^1 和 θ^2 均为估计量,若对于给定的 α(0<α<1) ,满足
P(θ^1≤θ≤θ^2)=1−α
,则称 [θ^1,θ^2] 为 θ 的置信度为 1−α 的置信区间。通过构造一个置信区间对未知参数进行估计的方法称为区间估计。
单个正态总体的区间估计
设 X1,X2,⋯,Xn 为来自总体 N(μ,σ2) 的样本,则
(1) 当 σ2 已知时, μ 的置信度为 1−α 的置信区间为
[X−nσu2α,X+nσu2α]
(2) 当 σ2 未知时, μ 的置信度为 1−α 的置信区间为
[X−nSt2α(n−1),X+nSt2α(n−1)]
(3) 当 μ 已知时, σ2 的置信度为 1−α 的置信区间为
[χ2α2(n)∑i=1n(Xi−μ)2,χ1−2α2(n)∑i=1n(Xi−μ)2]
(4) 当 μ 未知时, σ2 的置信度为 1−α 的置信区间为
[χ2α2(n−1)(n−1)S2,χ1−2α2(n−1)(n−1)S2]
双正态总体的区间估计
设 X∼N(μ1,σ12),X1,X2,⋯,Xn1 为其样本, Y∼N(μ2,σ22),Y1,Y2,⋯,Yn2 为其样本,且 X 与 Y 独立。
(1). 当 σ12,σ22 都已知时: μ1−μ2 的 1−α 的置信区间为
X−Y−u2αn1σ12+n2σ22,X−Y+u2αn1σ12+n2σ22
(2). 当 σ12,σ22 都未知时: μ1−μ2 的 1−α 的置信区间为
X−Y−t2α(γ)n1S12+n2S22,X−Y+t2α(γ)n1S12+n2S22
其中
γ=n12(n2−1)S14+n22(n1−1)S24(n1S12+n2S22)2
警告
特殊情形:
① σ12,σ22 未知,但 n1,n2 较大时: μ1−μ2 的 1−α 的置信区间为
Xˉ−Yˉ−u2αn1S12+n2S22, Xˉ−Yˉ+u2αn1S12+n2S22
② σ12=σ22=σ2 未知: μ1−μ2 的 1−α 的置信区间为
[Xˉ−Yˉ−t2αSwn11+n21, Xˉ−Yˉ+t2αSwn11+n21]
其中
Sw2=n1+n2−2(n1−1)S12+(n2−1)S22
t 分布为 t(n1+n2−2) 。
- μ1,μ2 已知: σ22σ12 的 1−α 的置信区间为
[∑n2=1n2(Yj−μ2)2∑n1=1n1(Xi−μ1)2F1−2α(n2,n1),∑n2=1n2(Yj−μ2)2∑n1=1n1(Xi−μ1)2F2α(n2,n1)]
(0−1) 分布无参数的区间估计
设总体 X∼(0−1) 分布, P{X=1}=p,P{X=0}=1−p,X1,X2,⋯,Xn(n≥50) 为其样本,则 p 的 1−α 的置信区间为
[Xˉ−u2αnXˉ(1−Xˉ),Xˉ+u2αnXˉ(1−Xˉ)]
单侧置信区间
设 θ 为总体的未知参数,对于给定值 α(0<α<1) ,若 P{θ≤θ}=1−α ,则称 (θ,+∞)
· 单侧置信区间
为 θ 的满足置信度 1−α 的单侧置信区间, θ 称为单侧置信下限。若 P{θ≤θˉ}=1−α ,则称 (−∞,θˉ] 为 θ 的满足置信度 1−α 的单侧置信区间, θ 称为单侧置信上限。
例如,对于正态分布 N(μ,σ2) , σ2 未知,可得 μ 的置信水平为 1−α 的单侧置信区间为
(−∞,Xˉ+tα(n−1)nS)
单侧置信上限为
μ=Xˉ+tα(n−1)nS
(Xˉ−tα(n−1)nS,+∞)
单侧置信下限为
μ=Xˉ−tα(n−1)nS
亦即只需将双侧置信区间的上、下限中的“ 2α ”改成“ α ”,就得到相应的单侧置信区间的上限或下限了。
· 习题
/example/ 设 X1,X2,⋯,Xn 为总体 X 的一个样本,求下列概率密度中未知参数 θ 的矩估计量和最大似然估计量。
概率密度函数:
f(x)={θ⋅2θx−(θ+1),0,x>2,others
其中 θ>1。
[矩估计].
计算总体期望:
μ=∫2∞xθ2θx−(θ+1)dx=θ−12θ
解得 θ 与 μ 的关系:
θ=μ−2μ
用样本均值 Xˉ 代替 μ,得到矩估计量:
θ^=Xˉ−2Xˉ
[最大似然估计].
构建似然函数:
L=(θ2θ)n(i=1∏nXi)−(θ+1)
取对数似然函数:
lnL=n(lnθ+θln2)−(θ+1)ln(i=1∏nXi)
对 θ 求导并令导数为零:
dθdlnL=n(θ1+ln2)−i=1∑nlnXi=0
解得最大似然估计量:
θ^=(n1∑i=1nlnXi−ln2)1
/example/
概率密度函数:
f(x)={θxθ−1,0,0≤x≤1,others
其中 θ>0。
[矩估计].
计算总体期望:
μ=∫01xθxθ−1dx=θ+1θ
解得 θ 与 μ 的关系:
θ=(1−μμ)2
用样本均值 Xˉ 代替 μ,得到矩估计量:
θ^=(1−XˉXˉ)2
[最大似然估计].
构建似然函数:
L=θn/2(i=1∏nXi)θ−1
取对数似然函数:
lnL=2nlnθ+(θ−1)i=1∑nlnXi
对 θ 求导并令导数为零:
dθdlnL=2θn+2θ1i=1∑nlnXi=0
解得最大似然估计量:
θ^=(∑i=1nlnXi)2n2
Part 4 假设检验
· 假设检验的基本概念
假设检验
对总体的分布类型或分布中的未知参数作出假设,然后抽取样本并选择一个合适的检验统计量,利用检验统计量的观察值和预先给定的误差 α ,对所作假设成立与否作出定性判断,这种统计推断称为假设检验。
若总体分布已知,只对分布中未知参数提出假设并作检验,这种检验称为参数检验。
假设检验基本思想的依据是小概率原理
小概率原理是指概率很小的事件在试验中发生的频率也很小,因此小概率事件在一次试验中几乎不可能发生。
当对问题提出待检假设 H0 ,并要检验它是否可信时,先假定 H0 正确。在这个假定下,经过一次抽样,若小概率事件发生了,就作出拒绝 H0 的决定;否则,若小概率事件未发生,则接受 H0 。
假设检验基本概念
在显著性水平 α 下,检验假设
H0:μ=μ0,H1:μ=μ0,
当检验统计量取某个区域 C 中的值时,我们拒绝原假设 H0 ,则称区域 C 为拒绝域(或否定域)。
假设检验过程
- 提出原假设和备择假设;
- 选取检验统计量;
- 确定拒绝原假设的域;
- 计算检验统计量的观察值并作出判断。
两类错误
人们作出判断的依据是一个样本,样本是随机的,因而人们进行假设检验判断 H0 可信与否时,不免因误判而犯两类错误:
- 第一类错误: H0 为真,而检验结果将其否定,这称为“弃真”错误;
- 第二类错误: H0 不真,而检验结果将其接受,这称为“取伪”错误。 分别记犯第一、二类错误的概率为 α,β ,即 α=P{ 拒绝 H0∣H0 为真 }, β=P{ 接受 H0∣H0 不真 } 。当样本容量 n 固定时, α 越小, β 就越大。一般采取的原则是:固定 α ,通过增加样本容量 n 降低 β
假设检验与区间估计的联系 假设检验与区间估计是从不同角度对同一问题的回答,它们解决问题的途径是相通的。下面以正态总体 N(μ,σ2) ,其中 σ2 已知,关于 μ 的假设检验和区间估计为例加以说明:
假设 H0:μ=μ0 ,当 H0 为真时,则 U=σ/nXˉ−μ0∼N(0,1) ,对于给定的显著性水平 α , P{∣U∣≤u2α}=1−α ,那么 H0 的接受域为
(Xˉ±u2αnσ0)
即认为以 1−α 的概率接受 H0 ,事实上,这个接受域也是 μ 的置信度为 1−α 的置信区间。这充分说明两者解决问题的途径相同,假设检验判断的是结论是否成立,而参数估计解决的是范围问题。
· 正态总体参数的假设检验
一个正态总体的假设检验
设 X∼N(μ,σ2),(X1,X2,⋯,Xn) 为其样本,
(1) σ2 已知,检验假设 H0:μ=μ0,H1:μ=μ0 。检验步骤为:
提出待检验假设 H0:μ=μ0(μ0 已知);
选取样本 (X1,X2,⋯,Xn) 的统计量
U=σ0/nXˉ−μ0
( σ0 已知),在 H0 成立时, U∼N(0,1) ;
对给定的显著性水平 α ,查表确定临界值 u2α ,使得
P{∣U∣>u2α}=α
计算检验统计量 U 的观察值并与临界值 u2α 比较;
作出判断:若 ∣U∣>u2α ,则拒绝 H0 ;若 ∣U∣≤u2α ,则接受 H0 。
(2) σ2 未知,检验假设
H0:μ=μ0,H1:μ=μ0
选取统计量
T=S/nXˉ−μ0
其中
S2=n−11i=1∑n(Xi−Xˉ)2
当 H0 为真时, T∼t(n−1) ,拒绝域为 ∣T∣>t2α(n−1) 。
(3) μ 已知,检验假设
H0:σ2=σ02,H1:σ2=σ02
选取统计量
χ2=σ02∑i=1n(Xi−μ0)2∼χ2(n)
拒绝域为 χ2>χ2α2(n) 或 χ2<χ1−2α2(n) 。
(4) μ 未知,检验假设
H0:σ2=σ02,H1:σ2=σ02
选取统计量
χ2=σ02(n−1)S2
当 H0 为真时, χ2∼χ2(n−1) ,拒绝域为 χ2>χ2α2(n−1) 或 χ2<χ1−2α2(n−1) 。
两个正态总体的假设检验
设 X∼N(μ1,σ12) , Y∼N(μ2,σ22) , (X1,X2,⋯,Xn1) 和 (Y1,Y2,⋯,Yn2) 分别是来自总体 X 和 Y 的样本, Xˉ,S12 和 Yˉ,S22 是相应的样本均值和样本方差
(1) σ12,σ22 已知,检验假设 H0:μ1=μ2,H1:μ1=μ2 。
选取统计量
U=n1σ12+n2σ22Xˉ−Yˉ∼N(0,1),
拒绝域为 ∣U∣>u2α 。
(2) σ12,σ22 未知,检验假设 H0:μ1=μ2,H1:μ1=μ2 。常见的三种特殊情况:
① 当 n1,n2 较大时:选取统计量
U=n1S12+n2S22Xˉ−Yˉ∼N(0,1),
拒绝域为 ∣U∣>u2α 。
② σ12=σ22 时:选取检验统计量
T=n1+n2−2(n1−1)S12+(n2−1)S22(n11+n21)Xˉ−Yˉ,
当 H0 为真时, T∼t(n1+n2−2) ,显著性水平为 α 的拒绝域为 ∣T∣>t2α(n1+n2−2) 。
③ σ12=σ22 ,但 n1=n2 (配对问题):
令 Di=Xi−Yi(i=1,2,⋯,n) ,则 Di∼N(μD,σD2) ,其中 μD=μ1−μ2,σD2=σ12+σ22 (未知)。此时检验假设等价于 H0:μD=0,H1:μD=0 。
选取统计量
T=SD/nDˉ−μD∼t(n−1),
拒绝域为 ∣T∣>t2α(n−1) 。
(3) μ1,μ2 已知,检验假设 H0:σ12=σ22,H1:σ12=σ22 。
选取统计量
F=(∑j=1n2(Yj−μ2)2)/n2(∑i=1n1(Xi−μ1)2)/n1∼F(n1,n2),
拒绝域为 F>F2α(n1,n2) 或 F<F1−2α(n1,n2) 。
(4) μ1,μ2 未知,检验假设 H0:σ12=σ22,H1:σ12=σ22 。
选取检验统计量
F=S22S12,
当 H0 为真时 F∼F(n1−1,n2−1) ,显著性水平为 α 的拒绝域为
F>F2α(n1−1,n2−1)或F<F1−2α(n1−1,n2−1)。
· 单侧检验
在假设检验中,如果只关心总体参数是否偏大或偏小,此时可将拒绝域确定在一侧,这种检验称为单侧检验。单侧检验可由双侧检验修改转化而得到。常用基本类型举例:
σ2 已知,检验假设
H0:μ≤μ0,H1:μ>μ0
有时也写成
H0:μ=μ0,H1:μ>μ0
选取
U=σ/nXˉ−μ0
拒绝域为
U>uα
σ2 已知,检验假设
H0:μ≥μ0,H1:μ<μ0
选取
U=σ/nXˉ−μ0
拒绝域为
U<−uα
σ2 未知,检验假设
H0:μ≤μ0,H1:μ>μ0
选取
T=S/nXˉ−μ0
拒绝域为
T>tα(n−1)
σ2 未知,检验假设
H0:μ≥μ0,H1:μ<μ0
选取
T=S/nXˉ−μ0
拒绝域为
T<−tα(n−1)
μ 未知,检验假设
H0:σ2≤σ02,H1:σ2>σ02
选取
χ2=σ02(n−1)S2
拒绝域为
χ2>χα2(n−1)
μ 未知,检验假设
H0:σ2≥σ02,H1:σ2<σ02
选取
χ2=σ02(n−1)S2
拒绝域为
χ2<χ1−α2(n−1)
μ1,μ2 未知,检验假设
H0:σ12≤σ22,H1:σ12>σ22
选取
F=S22S12
拒绝域为
F>Fα(n1−1,n2−1)
μ1,μ2 未知,检验假设
H0:σ12≥σ22,H1:σ12<σ22
选取
F=S22S12
拒绝域为
F<F1−α(n1−1,n2−1)
结束.
更新日志
2025/11/26 14:37
查看所有更新日志
fdf57-vector于c1b47-applied-mechanics于f41af-statistics于1595c-meta于348a6-add statistics于c9ee8-plume于a28aa-a于