· 关于电控的学习路径

试想机械拿来一台并不完善的平衡步兵给你来调，其中的很多参数甚至都不能完全确定，这个时候作为只是做完任务并掌握了一点的Git的电控小灯你能做点什么？

你希望搞明白学长传承的框架，演算机械的一些参数保证机械在缅北强度的工作下不往结构里面掺shit，那我想下面应该做一点这样的微博的工作罢：

首先你要把机械给出的理论模型用MATLAB去做演算，用Laplace变换将相关的微分方程化成代数方程求出PID的参数符合什么样的标准（当然代码有相关的Library），或者用LQR线性二次型调节器进行解算；

然后你需要在已有的电控框架里面调整电机的参数，使其能够接受通信信号，并在代码框架里面尝试写出依托符合战队代码规范的shit（譬如变量命名不要有拼音，然后要有注释，猫条你作为代码小白产出的多少的shit你自己一定是知道的罢），并确定里面没有任何error这种让人恼火的东西

然后是整车的布线，这里要注意焊接的规范和串口的使用，要是搞不好的话会出现一些很有节目效果的东西（“妙妙机械拿给电控看，电控嘎巴一下似了”）

最后就是烧录和debug的部分了.

"交给电控就好了，反正他们会调的"

· 关于平衡步兵

还是换成night主题写markdown舒服口牙

我们先引用王天威老师书中的一段话

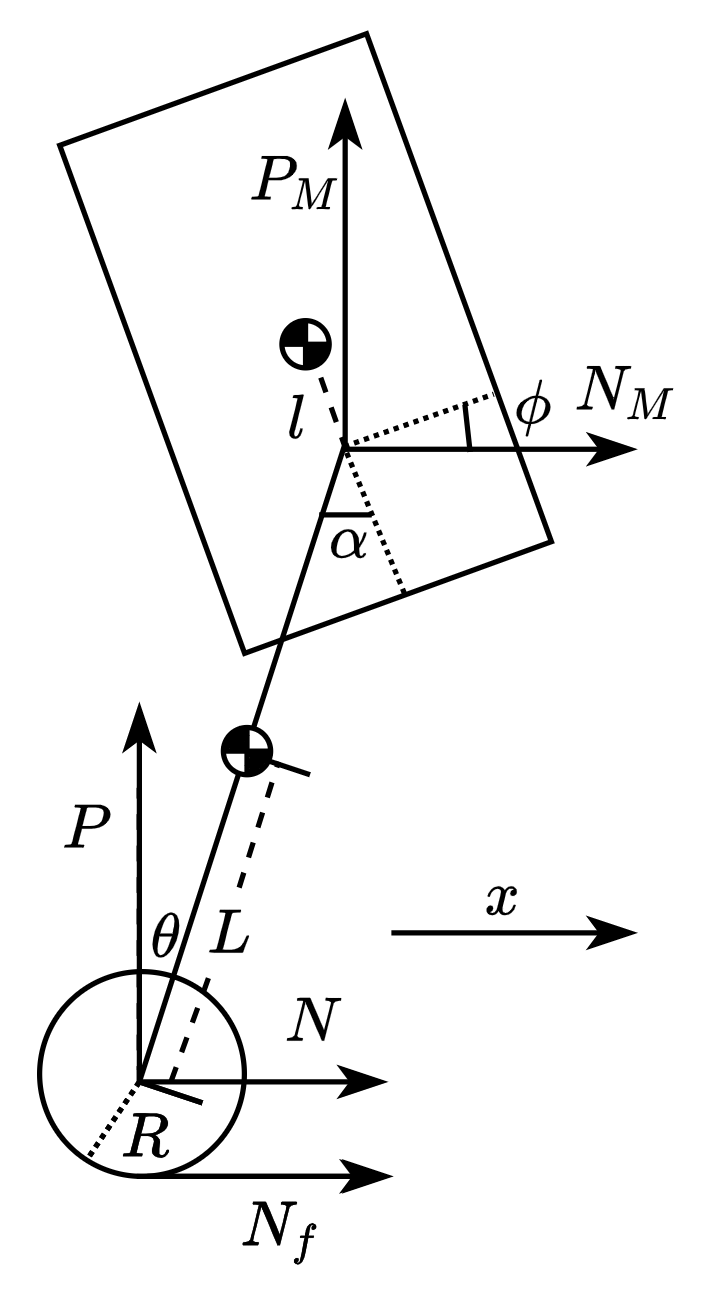
平衡车可以通过人体的姿态自动调整前后平衡，使驾驶者可以在不失去平衡的情况下行驶. 当只考虑它在二维平面移动时，可以将其简化为一个倒立摆的数学模型.

简化后的模型包括一个质量为 $m$ 的小球，一个长度为 $d$、质量忽略不计的连杆，以及一个可以水平移动的小车，其质量同样忽略不计. 系统的受力分析已在图中标出. 其中，$\phi_{(t)}$ 是连杆小球与竖直方向的夹角，$\xi_{(t)}$ 是小车的位移. 下面对连杆小球进行受力分析.

在 $x$ 方向，根据牛顿第二定律，有

$$m \frac{\mathrm{d}^2 x_{(t)}}{\mathrm{d}t^2} = F_{x_{(t)}} \quad (3.3.1)$$

其中，$x_{(t)}$ 是小球沿 $x$ 方向的相对地面的全局位移，它由小车的位移与小球相对于小车的位移组成，可以表达为

$$x_{(t)} = \xi_{(t)} + d \sin\phi_{(t)} \quad (3.3.2)$$

对其进行线性化处理，当 $\phi_{(t)}$ 较小时，$\sin\phi_{(t)} \approx \phi_{(t)}$. 代入式 (3.3.2)，并对等号两边取二次微分，可以得到

$$\frac{\mathrm{d}^2 x_{(t)}}{\mathrm{d}t^2} = \frac{\mathrm{d}^2 \xi_{(t)}}{\mathrm{d}t^2} + d \frac{\mathrm{d}^2 \phi_{(t)}}{\mathrm{d}t^2} \quad (3.3.3)$$

代入式 (3.3.1)，得到

$$m \frac{\mathrm{d}^2 \xi_{(t)}}{\mathrm{d}t^2} + m d \frac{\mathrm{d}^2 \phi_{(t)}}{\mathrm{d}t^2} = F_{x_{(t)}} \quad (3.3.4)$$

等号右边的 $F_{x_{(t)}}$ 是平衡车对连杆在 $x$ 方向的分力，即 $F_{x_{(t)}} = F_{(t)} \sin\phi_{(t)}$，当 $\phi_{(t)}$ 较小时，$\sin\phi_{(t)} \approx \phi_{(t)}$，即 $F_{x_{(t)}} = F_{(t)} \phi_{(t)}$，代入式 (3.3.4)，得到 $x$ 方向的动态方程

$$m \frac{\mathrm{d}^2 \xi_{(t)}}{\mathrm{d}t^2} + m d \frac{\mathrm{d}^2 \phi_{(t)}}{\mathrm{d}t^2} = F_{(t)} \phi_{(t)} \quad (3.3.5)$$

在 $y$ 方向，小球的重力与连杆在 $y$ 方向的分力相等，即 $mg = F_{y_{(t)}} = F_{(t)} \cos\phi_{(t)}$，当 $\phi_{(t)}$ 较小时，$\cos\phi_{(t)} \approx 1$，即在 $y$ 方向

$$mg = F_{(t)} \cos\phi_{(t)} = F_{(t)} \quad (3.3.6)$$

将式 (3.3.6) 代入式 (3.3.5)，整理后可以得到连杆小球关于角度 $\phi_{(t)}$ 的动态方程，即

$$\frac{\mathrm{d}^2 \phi_{(t)}}{\mathrm{d}t^2} - \frac{g}{d} \phi_{(t)} = -\frac{1}{d} \frac{\mathrm{d}^2 \xi_{(t)}}{\mathrm{d}t^2} \quad (3.3.7)$$

构建系统的状态空间方程，定义状态变量 $x_{(t)} = \begin{bmatrix} x_{1_{(t)}} & x_{2_{(t)}} \end{bmatrix}^\mathrm{T}$，则

$$x_{1_{(t)}} = \phi_{(t)} \quad (3.3.8a)$$

$$x_{2_{(t)}} = \frac{\mathrm{d}x_{1_{(t)}}}{\mathrm{d}t} = \frac{\mathrm{d}\phi_{(t)}}{\mathrm{d}t} \quad (3.3.8b)$$

定义系统输入为

$$u_{(t)} = -\frac{1}{d} \frac{\mathrm{d}^2 \xi_{(t)}}{\mathrm{d}t^2} \quad (3.3.8c)$$

其中，$\dfrac{\mathrm{d}^2 \xi_{(t)}}{\mathrm{d}t^2}$ 是平衡车沿水平方向的加速度，它与平衡车电动机的转速相关. 将其乘以 $-\dfrac{1}{d}$ 使其单位化.

取 $x_{2_{(t)}}$ 对时间的导数并结合式 (3.3.8c)，共同代入式 (3.3.7) 可得F

$$\frac{\mathrm{d}x_{2_{(t)}}}{\mathrm{d}t} = \frac{\mathrm{d}^2 \phi_{(t)}}{\mathrm{d}t^2} = \frac{g}{d} \phi_{(t)} + u_{(t)} = \frac{g}{d} x_{1_{(t)}} + u_{(t)} \quad (3.3.9)$$

将式 (3.3.8b) 和式 (3.3.9) 写成一个紧凑的矩阵表达形式，可以得到系统的状态空间方程

$$\begin{bmatrix} \dfrac{\mathrm{d}x_{1_{(t)}}}{\mathrm{d}t} \\ \dfrac{\mathrm{d}x_{2_{(t)}}}{\mathrm{d}t} \end{bmatrix} = \frac{\mathrm{d}x_{(t)}}{\mathrm{d}t} = \begin{bmatrix} 0 & 1 \\ \dfrac{g}{d} & 0 \end{bmatrix} x_{(t)} + \begin{bmatrix} 0 \\ 1 \end{bmatrix} u_{(t)} \quad (3.3.10)$$

系统的控制目标是当连杆小球的位置受到扰动偏离中心时，通过控制小车的加速度使其回到平衡位置. 因此本系统的目标状态量 $x_d = \begin{bmatrix} x_{1d} & x_{2d} \end{bmatrix}^\mathrm{T} = \begin{bmatrix} 0 & 0 \end{bmatrix}^\mathrm{T}$. 这是一个调节控制问题.

其性能指标可以定义为

$$J = \int_{t_0}^{t_f} (\|x_{(t)}\|_Q^2 + \|u_{(t)}\|_R^2)\,\mathrm{d}t \quad (3.3.11)$$

式 (3.3.11) 选取了运行代价与系统输入的组合. 其中运行代价选择的是状态变量 $x_{(t)}$ 与目标 $\mathbf{0}$ 的差值，这样的设定可以使系统在运行过程中状态变量 $x_{(t)}$ 始终向 $\mathbf{0}$ 靠拢.

权重矩阵 $Q$ 是一个常数矩阵 $Q = \begin{bmatrix} q_1 & 0 \\ 0 & q_2 \end{bmatrix}$.

在本例中输入只有一个变量，因此 $R$ 是一个一维的权重矩阵. 当系统偏离平衡位置后，输入会作用在系统上直到它回到平衡位置，之后则保持为零. 因此输入 $u_{(t)}$ 的代价直接体现了能耗的大小. 末端时间 $t_f$ 的选择也非常重要，在判断性能指标时，$t_f$ 需要足够长以保证系统已经回到平衡点位置. 至此，我们成功建立了平衡车控制问题的性能指标函数.

......

我们已经得到了简化倒立摆系统的状态空间方程，即

$$\frac{\mathrm{d}x_{(t)}}{\mathrm{d}t} = A x_{(t)} + B u_{(t)} \quad (4.4.48a)$$

$$A = \begin{bmatrix} 0 & 1 \\ \dfrac{g}{d} & 0 \end{bmatrix}, \quad B = \begin{bmatrix} 0 \\ 1 \end{bmatrix} \quad (4.4.48b)$$

其中，$x_{(t)} = \begin{bmatrix} x_{1_{(t)}} & x_{2_{(t)}} \end{bmatrix}^\mathrm{T}$ 分别代表了小球参考竖直方向的角度与角速度. 输入 $u_{(t)}$ 是单位化后的小车加速度. 假设在初始位置时系统的状态变量为 $x_{(t_0)} = \begin{bmatrix} \phi_0 & 0 \end{bmatrix}^\mathrm{T} = \begin{bmatrix} \dfrac{\pi}{20} & 0 \end{bmatrix}^\mathrm{T}$，即与竖直方向的角度为 $\dfrac{\pi}{20}$，角速度为 0. 控制的目标是令系统回归到平衡状态. 这是一个调节控制问题，定义性能指标为

$$J = \frac{1}{2} \int_{t}^{t_f} (x^\top_{(t)} Q x_{(t)} + u^\top_{(t)} R u_{(t)}) \,\mathrm{d}\tau \quad (4.4.49)$$

其中，$Q = \begin{bmatrix} q_1 & 0 \\ 0 & q_2 \end{bmatrix}$ 为小球角度与角速度的权重矩阵. 因为是单输入系统，因此 $R$ 为一维的权重矩阵.

对于这一问题，可以采用式 (4.4.40c)，得到

$$0 = P A + A^\top P - P B R^{-1} B^\top P + Q \quad (4.4.50)$$

在求解出 $P$ 之后可以使用式 (4.4.41) 得到反馈控制策略：

$$u^*_{(t)} = -R^{-1} B^\top P x_{(t)} = -K x_{(t)} \quad (4.4.51)$$

......

这就是平衡步兵口牙（划掉）

下面我们讲讲实操. 猫条sensei这两天心情很不愉快——自从18号回来之后开始调并腿平衡步兵就很不愉快，一方面是我cpp的水平太烂了，另一方面平步的控制逻辑并不那么好理解，下面我就按照自己的理解简单捋一下.

首先系统的控制离不开其本身具有的物理特性，但是车本身的受力结构复杂，所以我们必须予以简化，根据对称性我们可以简化为下图的模式（记住它，等会会用）

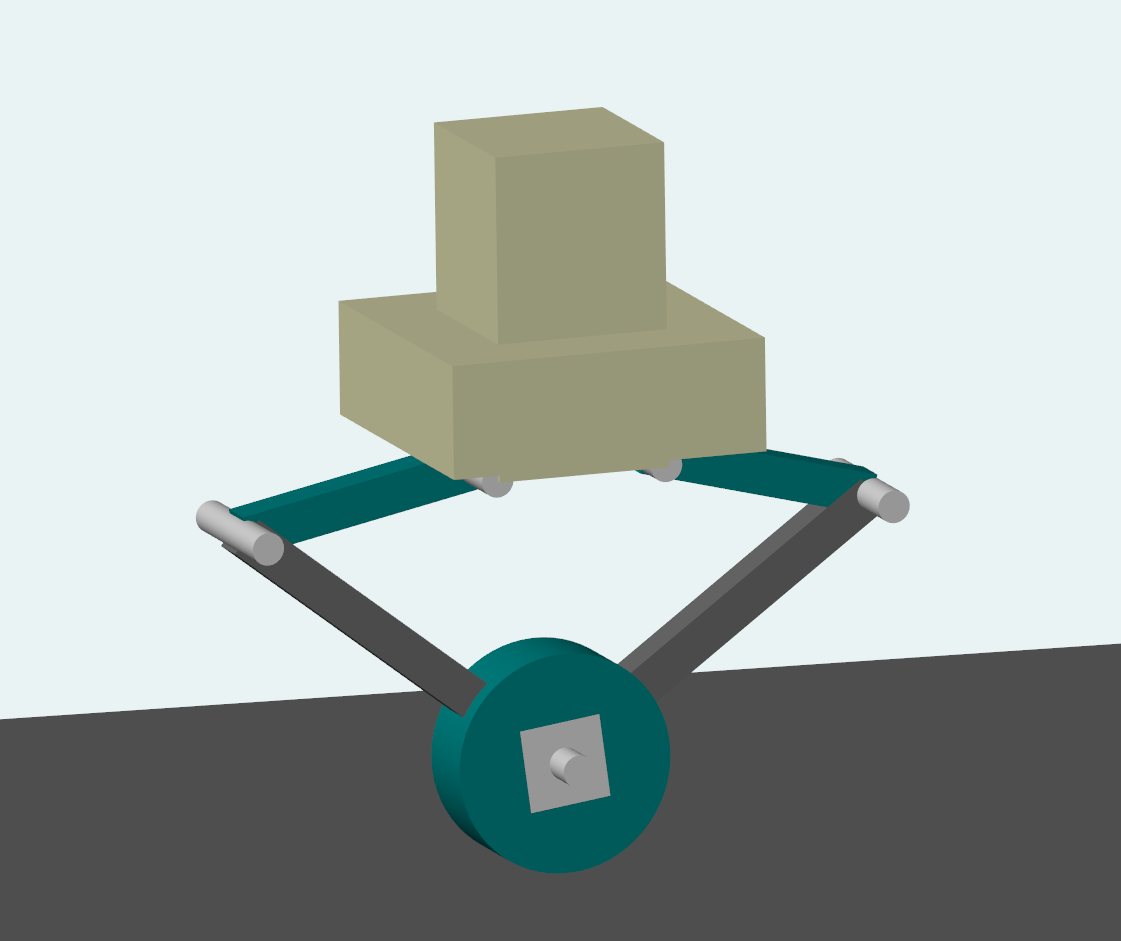
与此同时，我们知道：“对于机器人平衡与纵向运动问题，主要关注机器人上层机构与腿部的姿态以及驱动轮的运动，并忽略机器人腿长变化，仅考虑腿的姿态，即驱动轮轴与腿部两关节电机转轴中心的连线相对惯性系的角度. ”

所以我们可以简化为平面倒立摆结构.

从工程实践的角度来看，为平衡步兵这样的系统选择控制策略，首先会考虑经典的PID控制，因为它直观且易于实现. 然而，平衡步兵本质上是一个空间倒立摆，它是一个多变量、强耦合且内部不稳定的系统. 这意味着我们需要同时、协调地控制多个状态，比如车体的位移、速度以及摆杆的角度、角速度，这些状态在动力学上紧密关联，相互影响. 传统的PID控制器通常针对单输入单输出设计，当被强行用于此类多变量系统时，往往通过多个回路单独控制，难以妥善处理状态间的动态耦合，其参数整定会变得复杂且缺乏系统性的优化理论指导，导致性能受限，难以在高性能要求下实现快速、稳定且节能的平衡.

因此，我们必须转向现代控制理论的范畴，采用基于状态空间模型的LQR方法. 其核心在于，首先建立系统的状态空间模型，用一个状态向量完整描述所有关键变量，用数学模型精确刻画它们之间的耦合关系以及控制输入如何影响它们. 这为整体分析和设计奠定了基础. 在此基础上，LQR通过求解一个优化问题来设计控制器，它的目标是寻找一个控制律，使得一个综合了状态误差和控制代价的二次型性能指标达到最小.

具体而言，这个性能指标函数要求我们在“快速消除姿态偏差”和“不过度消耗控制能量”之间进行最优权衡. 通过设定状态权重矩阵和控制权重矩阵，我们可以定量地指定对各项性能的重视程度. 随后，LQR算法会依据此权重和系统模型，自动计算出一个最优的状态反馈增益矩阵. 这个增益矩阵已经内在、最优地协调了所有状态变量之间的复杂相互作用，能够给出一个全局最优的控制指令，从而同时实现系统的稳定、快速响应和高效节能，这正是平衡步兵这类先进机器人系统所追求的精准控制目标.

然后我们就可以开始第一步：利用MATLAB去解算微分方程，计算增益矩阵 $K$ . 在平衡步兵的LQR控制器设计中，利用MATLAB进行计算是连接理论模型和实际控制的关键环节. 其核心步骤包括建立系统状态空间模型、设计权重矩阵、离散化处理，以及最终求解增益矩阵.

下面开始尝试设计代码实现.

我们默认学长留下来的圣遗物里面已经封装好了can_recieve，姿态解算，PID计算等任务和库（）

整体上在数据流通的方向上满足从观测器，状态机，再到控制器的模式.

观测器负责检测电机状态和IMU传感器，对电机编码器和IMU进行处理，并判断车体此时刻的状态.

状态机通过定义清晰的状态、事件和转换规则，将电机复杂的运行流程转化为一个可控、可预测的离散系统模型. 其核心价值在于，任何时刻电机都处于有限状态中的一个，只有当特定事件（如收到指令、检测到故障）发生时，才会按预定逻辑切换状态，从而执行相应的精确操作. 这种机制非常适合管理电机自上电、启动、运行到停止、故障处理等一系列时序严格、逻辑分立的任务. 在实际的电机控制系统中，状态机被具体化为多个精细的状态. 从系统设计角度看，采用状态机模式能带来显著优势. 它使代码结构高度模块化，每个状态的处理逻辑独立封装，便于开发、调试和维护. 同时，状态机明确定义了状态转换的条件，避免了非法操作，使得整个控制流程清晰严谨，有效防止逻辑混乱.

控制器（Controller）作为自动控制系统的核心“决策机构”，是指挥整个系统协调工作的关键装置. 它通过预定的程序或算法，对各种执行设备（如电动机）的启动、调速、制动等动作进行精确控制，或者对温度、压力、流量等过程变量进行自动调节.

下面我们讲讲控制器.

对于一个五连杆平衡步兵来说，我们可以简单把状态分为四种：倒地、站起与巡航和 报错，我们知道状态机在不同情况下会给出不同的控制逻辑，自然状态机会选择不同的控制器来使得车正常运行，但是注意，我们写的控制逻辑实际上是基于一阶倒立摆去进行撰写的，但是实际车的模型不同于一阶倒立摆，所以我们需要用VMC进行解算

一阶倒立摆模型在分析平衡控制的基本原理时非常有效，它将车辆简化为在平面内运动的一个质点和一根摆杆. 但真实车辆的运动涉及纵向、横向和横摆三个自由度的强耦合，以及轮胎力学的非线性特性、载荷转移、空气动力学效应等诸多复杂因素. 直接将在简化模型上整定好的控制器（如特定的PID控制器）应用于实车，往往难以获得稳定、精确的控制效果，因为简化模型无法准确反映所有这些复杂的相互作用.

并联腿平衡步兵是一个高度耦合、非线性的复杂系统. 虽然在控制器设计的初始阶段，我们常常基于简化的一阶倒立摆模型进行理论分析和算法选型（如LQR），但实际机器人的动力学特性远比简化模型复杂. 真实的并联腿结构涉及多个关节的协同运动，存在复杂的动力学耦合关系. 若直接将基于简化模型的控制器应用于实物，往往难以获得稳定、精确的性能，因为简化模型无法准确反映所有这些复杂的相互作用.

VMC（Virtual Model Control，虚拟模型控制）的核心思想是在机器人系统上构造一个虚拟的力学环境. 接下来的关键步骤，是通过雅可比矩阵将计算得到的工作空间虚拟力映射到各个关节的力矩指令上. VMC的优势在于，它允许工程师使用相对直观的“虚拟力”概念来设计机器人的整体运动行为，从而在一定程度上避免了对复杂、非线性且可能难以精确建模的系统动力学进行直接依赖.

在站起与巡航的模式下，我们需要用LQR控制车体的平衡，用PID控制 yaw 方向的平地旋转，虚拟杆的腿长，roll方向上左右腿长不等的情况，以及腿的摆角（包括左右腿劈叉的情况），在此之后用VMC翻译解算；在倒地的情况下，我们希望车能站起来，这时候我们使用PID控制腿长和起摆（一阶倒立摆，给轮子一个加速度），并用VMC翻译和解算.

这就是平衡步兵的控制逻辑.

电控好累，电控好难.

下面是引用部分，致敬我们的群主

版权所有

版权归属：nicostore-mathematica

许可证：署名-非商业性-相同方式共享 4.0 国际 (CC-BY-NC-SA-4.0)